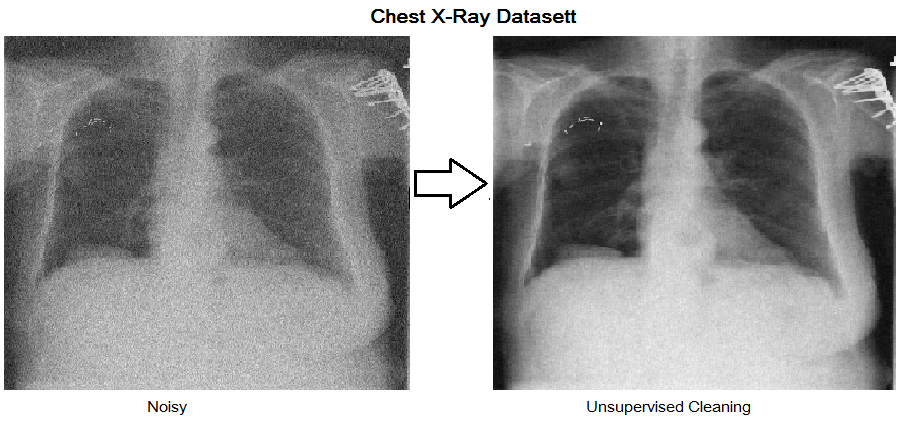
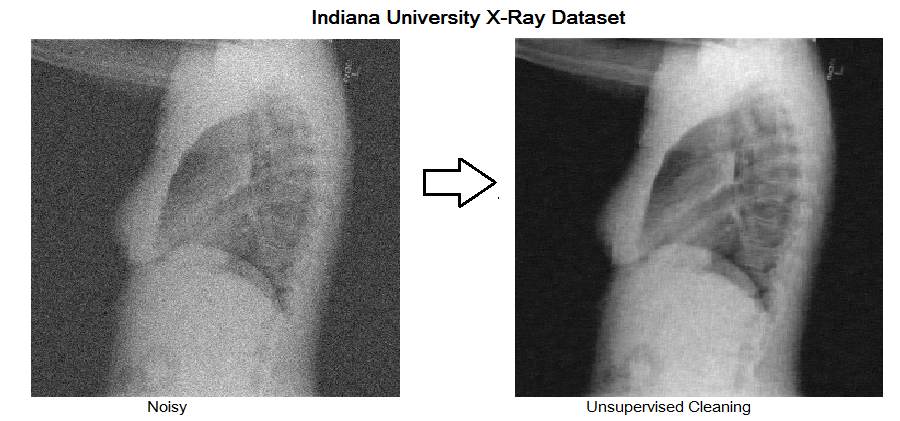




Among the plethora of techniques devised to curb the prevalence of noise in medical images, deep learning based approaches have shown most promise. However, one critical limitation of these deep learning based denoisers is the requirement of high quality noiseless ground truth images that are difficult to obtain in many medical imaging applications such as X-rays. To circumvent this issue, we leverage recently proposed approach of this paper that incorporates Stein's Unbiased Risk Estimator (SURE) to train a deep convolutional neural network without requiring denoised ground truth X-ray data.
We consider recovering true X-ray image $\boldsymbol{x} \in \mathbb{R}^m$ from its noisy measurements of the form \begin{equation} \boldsymbol{y} = \boldsymbol{x} + \boldsymbol{w}, \end{equation} where $\boldsymbol{y} \in \mathbb{R}^m$ is noise corrupted image, and $\boldsymbol{w} \in \mathbb{R}^m$ denote independent and identically distributed Gaussian noise i.e. $\boldsymbol{w} \sim \mathcal{N}(0,\sigma^2 \boldsymbol{I}) $ where $\boldsymbol{I}$ is identity matrix and $\sigma$ is standard deviation that is assumed to be known. We are interested in a weakly differentiable function $f_\theta(.)$ parameterized by $\theta$ that maps noisy X-ray images $\boldsymbol{y}$ to clean ones $\boldsymbol{x}$. We model $f_\theta(.)$ by a convolutional neural network (CNN) where $\theta$ are weights of this network. CNN based denoising methods are typically trained by taking a representative set of images $\boldsymbol{x}_1, \boldsymbol{x}_2, ...\boldsymbol{x}_L$, along with set of observations $\boldsymbol{y}_1, \boldsymbol{y}_2...\boldsymbol{y}_L$, either physically or using simulations. The network then learns the mapping $f_\theta : \boldsymbol{y} \rightarrow \boldsymbol{x}$ from observations back to images by minimizing a supervised loss function; typically mean-squared-error (MSE) is employed as shown below. \begin{equation} \label{eq:MSE} \underset{\theta}{\text{min}} \quad \sum_{\ell=1}^{L} \frac{1}{L} \Vert \boldsymbol{x}_{\ell} - f_\theta({\boldsymbol{y}_{\ell}}) \Vert^2. \end{equation} Note the dependence of MSE on ground truth images $\boldsymbol{x}$. Instead of optimizing MSE, we employ SURE loss whose objective function with respect to $\boldsymbol{w}$ can be written as \begin{equation} \label{eq:SURE} \sum_{\ell=1}^{L} \frac{1}{L} \Vert \boldsymbol{y}_{\ell} - f_\theta({\boldsymbol{y}_{\ell}}) \Vert^2 - \sigma_{w}^2 + \frac{2 \sigma_{w}^2}{n} \text{div}_{\boldsymbol{y}}{(f_\theta(\boldsymbol{y}))}, \end{equation} where $\text{div}(.)$ denotes divergence and is defined as \begin{equation} \text{div}_{\boldsymbol{y}}{(f_\theta(\boldsymbol{y})} = \sum_{\ell=1}^{L} \frac{\partial f_{\theta n} (\boldsymbol{y})}{\partial y_n} \end{equation} Calculating divergence of the denoiser is a central challenge for SURE based estimators. We estimate divergence via fast Monte Carlo approximation, see \citep{ramani2008monte} for details. In short, instead of utilizing a supervised loss of MSE in \ref{eq:MSE}, we optimize network weights $\boldsymbol{\theta}$ in an unsupervised manner using \ref{eq:SURE}, that does not require ground truth.
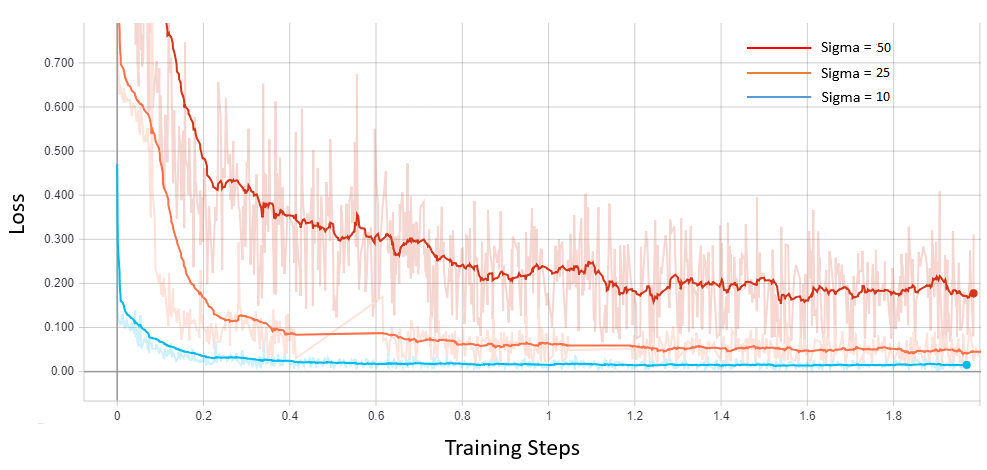
We use Indiana University’s Chest X-ray database for training. Database consists of 7470 chest X-ray images of varying size, out of which we select 500 images for training due to scarcity of computational resources. Training images are re-scaled, cropped and flipped, to form a set of 789760 overlapping patches each of size 40 × 40. We use different settings of hyperparameters including learning rate, number of layers, patch size etc. to find optimal values. We trained DnCNN network using SURE loss without any clean data on three different noise levels of 10, 25 and 50. Following figure shows SURE training loss curve for each noise level. Note that network easily converges for small variance noise while higher noise levels make the network hard to converge.
Quantitative denoising results for DnCNN trained using SURE loss and MSE loss for Gaussian noise with standard deviation of 25 and 50. Average values of PSNR, SSIM, and MSE are calculated for 10 images from a test set of Indiana University X-Ray dataset.
The table shows the performance of SURE based denoiser for two different datasets. SURE based model works comparably well although it does not require any clean dataset. Interestingly, denoiser trained on Indiana University X-Ray Dataset also works well on NIH Chest X-Ray Dataset.





